Go语言-数据结构

发表于 | 分类于 | 评论数： | 阅读次数：
本文字数： 17k | 阅读时长 ≈ 16 分钟

摘要

  • 图和节点
  • 分析算法复杂度
  • Go的二叉树
  • Go的哈希表
  • Go的链表
  • Go的双端链表
  • Go的队列
  • Go的栈
  • Go标准库container包提供的数据结构
  • Go生成随机数
  • 构建随机字符串用作难以破解的密码

图和节点

图G(V,E)是由一组有限的，非空的顶点集V（或者节点）以及一组边E组成。有两种主要的类型：有环图和无环图。有环图是指其全部或者部分顶点集存在闭环。在无环中，没有闭环。有向图是其边有方向性，有向无环图是没有闭环的有向图。

通常一个节点（node)包含很多信息，所以node一般使用Go的数据结构来实现

算法复杂度

算法的效率是由计算的复杂度来判定的，这主要是和算法完成工作需要访问其输入数据的次数有关。

在计算机科学中通常用大O表示法来描述算法的复杂度。因此，只需要访问线性次输入数据的O(n)算法要更优于O(n2)的算法以及O(n3)的算法等等。然而最坏的算法就是O(n!)，想输入超过300个元素是不可能的。

最后，Go大多数内置数据类型的查找操作，例如map中通过key查找value或者访问数组元素都是常量时间内完成即O(1)。这就意味着内置数据类型通常比自定义类型更快，所以你应该优先使用它们，除非你想完全控制幕后发生的事情。此外并非所有的数据结构都相同，通常来讲数组操作数据比map要快，这也是你必须为map的多功能性付出的代价。

尽管每种算法都有他的缺点，但是如果你的数据量不是很大的时候，只要算法能够准确的执行所需的工作，那么这些就不是很重要了。

二叉树

  • 二叉树是每个节点最多有两个两个分支的数据结构。“最多”表示一个节点可以连接一至两个子节点，或者不连接其他子节点。

  • 树的根节点是树结构中的第一个节点。

  • 树的深度，又称为树的高度，是从树的根节点到所有节点的路径中最长的一个。而节点的深度是该节点到树的根所经过的路径中边的数量。

  • 叶节点是没有子节点的节点。

若一个树的根节点到任意两个叶节点的距离之差不大于 1，则认为这个树是平衡的。顾名思义，非平衡树不是平衡的。树的平衡操作困难又缓慢，所以最好从一开始就让你的树保持平衡，而不是在建好树之后再去调整，尤其是这个树有很多节点的时候。

img

当你要描述多层次数据的时候，树是最好的选择。因此，树被广泛应用于编程语言的编译器解析计算机程序的过程。

此外，树本身就具有有序性，所以你不必另外对其进行排序。只要插入到了正确的位置，那么树就能保持有序。然而，由于树的构造方式，删除元素的操作有时至关重要。

如果一个二叉树是平衡的，它的查找、插入、删除操作需要 log(n) 步，这里的 n 是树上元素的总数量。此外，平衡二叉树的高度约为 log2(n)，这意味着一个拥有 10,000 个元素的平衡树的高度大约是 14。类似的，拥有 100,000 个元素的平衡树的高度大约是 17，拥有 1,000,000 个元素的平衡树的高度大约是 20。也就是说，向一个平衡二叉树中插入大量的元素后，对树进行操作的速度并不会大幅变化。换个说法，你只需要不到 20 步就能到达一个拥有 1,000,000 个节点的树上的任意一个节点！

二叉树最大的一个缺点是树的形状很依赖元素插入的顺序。如果树上元素的键又长又复杂，那么插入和查找元素的过程需要进行大量的匹配，从而变得很慢。最后，如果一个树不是平衡的，那么就很难对其性能进行预测。

尽管你能更快地创建链表或数组，但是二叉树在查找操作中的灵活性值得付出额外的开销并进行维护。在二叉树上查找一个元素时，你会比较要搜索的元素则值与当前节点值的大小，然后决定在哪个子树上继续搜索，这样做可以节约大量的时间。

Go实现的一个简单的二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
package main

import (
	"fmt"
	"math/rand"
	"time"
)

type Tree struct {
	Left  *Tree
	Value int
	Right *Tree
}

func traverse(t *Tree) {
	if t == nil {
		return
	}
	traverse(t.Left)
	fmt.Println(t.Value, " ")
	traverse(t.Right)
}

func create(n int) *Tree {
	var t *Tree
	rand.Seed(time.Now().Unix())
	for i := 0; i < 2*n; i++ {
		temp := rand.Intn(n * 2)
		t = insert(t, temp)
	}
	return t
}

func insert(t *Tree, v int) *Tree {
	if t == nil {
		return &Tree{nil, v, nil}
	}
	if v == t.Value {
		return t
	}
	if v < t.Value {
		t.Left = insert(t.Left, v)
		return t
	}
	t.Right = insert(t.Right, v)
	return t
}

func main() {
	tree := create(10)
	fmt.Println("The value of the root of the tree is", tree.Value)
	traverse(tree)
	fmt.Println()
	tree = insert(tree, -10)
	tree = insert(tree, -2)
	traverse(tree)
	fmt.Println()
	fmt.Println("The value of the root of the tree is", tree.Value)
}

哈希表

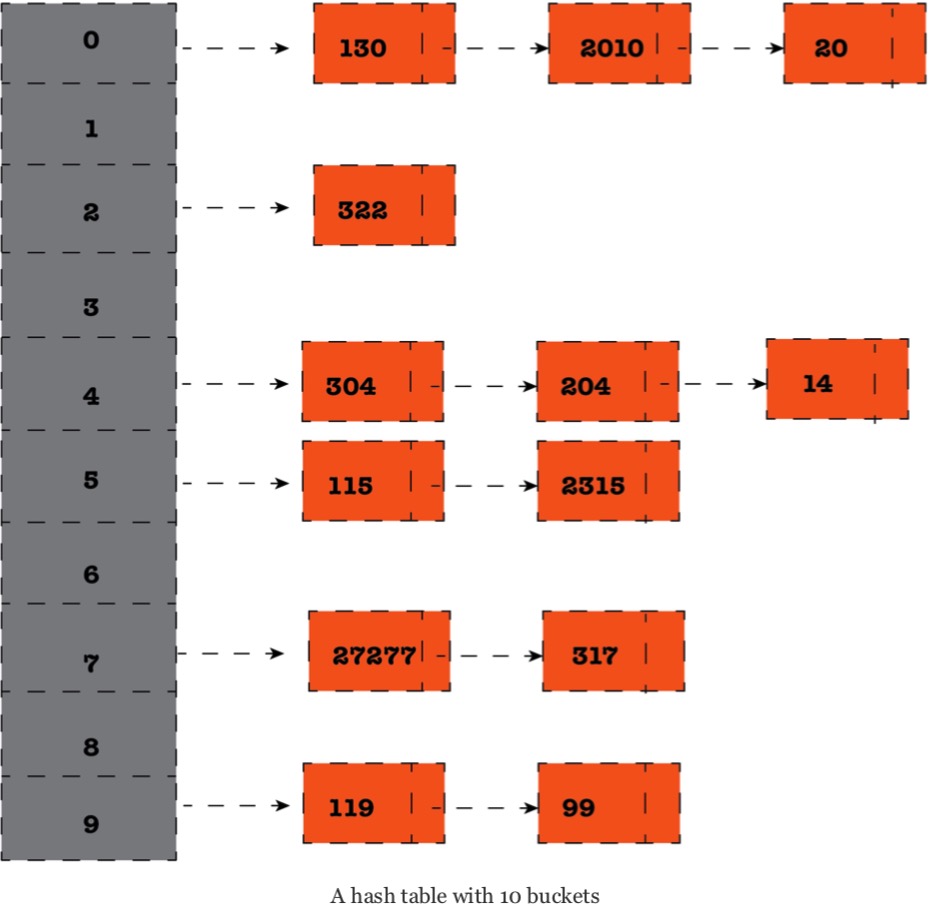
严格来讲，哈希表这种数据结构会存储一至多个键值对，并使用一个哈希函数计算出存放正确值的桶或槽的索引。理想情况下，哈希函数应该将每个键分配到唯一的桶中，但通常你事先得有足够数量的桶。

一个好的哈希函数一定要能够输出均匀分布的哈希值，如果有多余的桶或者桶之间的基数差值较大，操作的效率就会变低。此外，这个哈希函数应该具有一致性，对于同一个键始终输出相同的哈希值，否则就不能准确定位需要的数据。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
package main

import (
	"fmt"
)

const SIZE = 15

type Node struct {
	Value int
	Next  *Node
}

type HashTable struct {
	Table map[int]*Node
	Size  int
}

func hashFunction(i, size int) int {
	return (i % size)
}

func insert(hash *HashTable, value int) int {
	index := hashFunction(value, hash.Size)
	element := Node{Value: value, Next: hash.Table[index]}
	hash.Table[index] = &element
	return index
}

func traverse(hash *HashTable) {
	for k := range hash.Table {
		if hash.Table[k] != nil {
			t := hash.Table[k]
			for t != nil {
				fmt.Printf("%d -> ", t.Value)
				t = t.Next
			}
		}
		fmt.Println()
	}
}

func lookup(hash *HashTable, value int) bool {
	index := hashFunction(value, hash.Size)
	if hash.Table[index] != nil {
		t := hash.Table[index]
		for t != nil {
			if t.Value == value {
				return true
			}
			t = t.Next
		}
	}
	return false
}

func main() {
	table := make(map[int]*Node, SIZE)
	hash := &HashTable{Table: table, Size: SIZE}
	fmt.Println("Numbder of spaces:", hash.Size)
	for i := 0; i < 120; i++ {
		insert(hash, i)
	}
	traverse(hash)
	if lookup(hash,110) {
		fmt.Println(110)
	}
}

哈希表可以有效降低查找数据的次数

链表

链表是一种包含有限个元素的数据结构，其中每个元素至少占用两个存储单元，一个用于存储真正的数据，另一个用于存储链接当前元素和下一个元素的指针，从而建立了一个元素序列构成的链表。

链表中的第一个元素称为头，最后一个元素称为尾。在定义链表的过程中，你需要做的第一件事就是将链表头用单独的变量存储，因为链表头是你访问整个链表的唯一媒介。注意，如果弄丢了指向单向链表第一个节点的指针，你就没法再找到它了。

下图展示了一个拥有五个节点的链表：

img

下图描述了如何从链表中移除一个节点，它将帮助你更好地理解这个过程所涉及的步骤。你要做的主要是修改被删除节点左侧的那个节点，将它指向下一个元素的指针指向被删除节点右侧的那个节点。

img

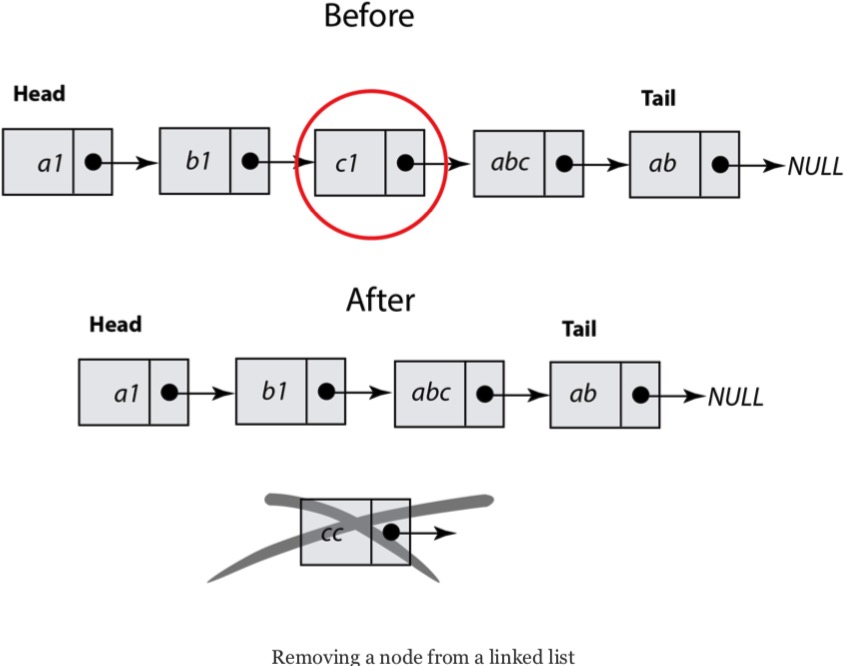
下面的链表实现已经相对简化了，并且不含删除节点的功能，这个功能的实现将留给读者作为练习题。

依据工作原理，链表通常不含重复的项。此外，如果不是有序链表，新的节点通常会被添加在链表的尾部。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
package main

import (
	"fmt"
)

type Node struct {
	Value int
	Next  *Node
}

var root = new(Node)

func addNode(t *Node, v int) int {
	if root == nil {
		t = &Node{v, nil}
		root = t
		return 0
	}

	if v == t.Value {
		fmt.Println("Node already exists:", v)
		return -1
	}

	if t.Next == nil {
		t.Next = &Node{v, nil}
		return -2
	}

	return addNode(t.Next, v)
}

func traverse(t *Node) {
	if t == nil {
		fmt.Println("-> Empty list!")
		return
	}

	for t != nil {
		fmt.Printf("%d -> ", t.Value)
		t = t.Next
	}
	fmt.Println()
}

func lookupNode(t *Node, v int) bool {
	if root == nil {
		t = &Node{v, nil}
		root = t
		return false
	}

	if v == t.Value {
		return true
	}

	if t.Next == nil {
		return false
	}

	return lookupNode(t.Next, v)
}

func size(t *Node) int {
	if t == nil {
		fmt.Println("-> Empty list!")
		return 0
	}

	i := 0
	for t != nil {
		i++
		t = t.Next
	}
	return i
}

func main() {
	fmt.Println(root)
	root = nil
	traverse(root)
	addNode(root, 1)
	addNode(root, -1)
	traverse(root)
	addNode(root, 10)
	addNode(root, 5)
	addNode(root, 45)
	addNode(root, 5)
	addNode(root, 5)
	traverse(root)
	addNode(root, 100)
	traverse(root)

	if lookupNode(root, 100) {
		fmt.Println("Node exists!")
	} else {
		fmt.Println("Node does not exist!")
	}

	if lookupNode(root, -100) {
		fmt.Println("Node exists!")
	} else {
		fmt.Println("Node does not exist!")
	}
}

链表最大的优点就是容易理解和实现。链表的通用性使得它们可以用于很多不同的情形。这意味着可以用链表对各种不同类型的数据建模。此外，在链表中使用指针进行顺序检索的速度非常快。

链表不仅可以对数据排序，还可以在插入和删除元素之后保持数据的有序性。从有序链表中删除一个节点的操作与无序链表中相同，而向有序链表中插入新的节点则与无序链表中不同，为了保持链表的有序性，必须将新节点放到正确的位置。实际上，这意味着如果你有大量数据并且会频繁删除数据，那么相对于哈希表和二叉树，使用链表是一个更好的选择。

最后，有很多技术可以优化有序链表中搜索和查找节点的过程。其中最常用的一种就是保存一个指向有序链表中间节点的指针，之后每次都从这个节点开始查找。这个简单的优化方法可以将查找操作的时间减少一半！

双向链表

双向链表中的每个节点都既有指向前一个元素的指针，又有指向下一个元素的指针。

双向链表形如下图：

img

因此，在一个双向链表中，第一个节点的后链接指向第二个节点，而它的前链接指向 nil（也称为 NULL）。类似的，最后一个节点的后链接指向 nil，而它的前链接指向双向链表中的倒数第二个节点。

本章的最后一个插图阐明了双向链表中增加节点的操作。可想而知，这个过程中的主要任务是处理新节点、新节点左侧节点、新节点右侧节点这三个节点的指针。

img

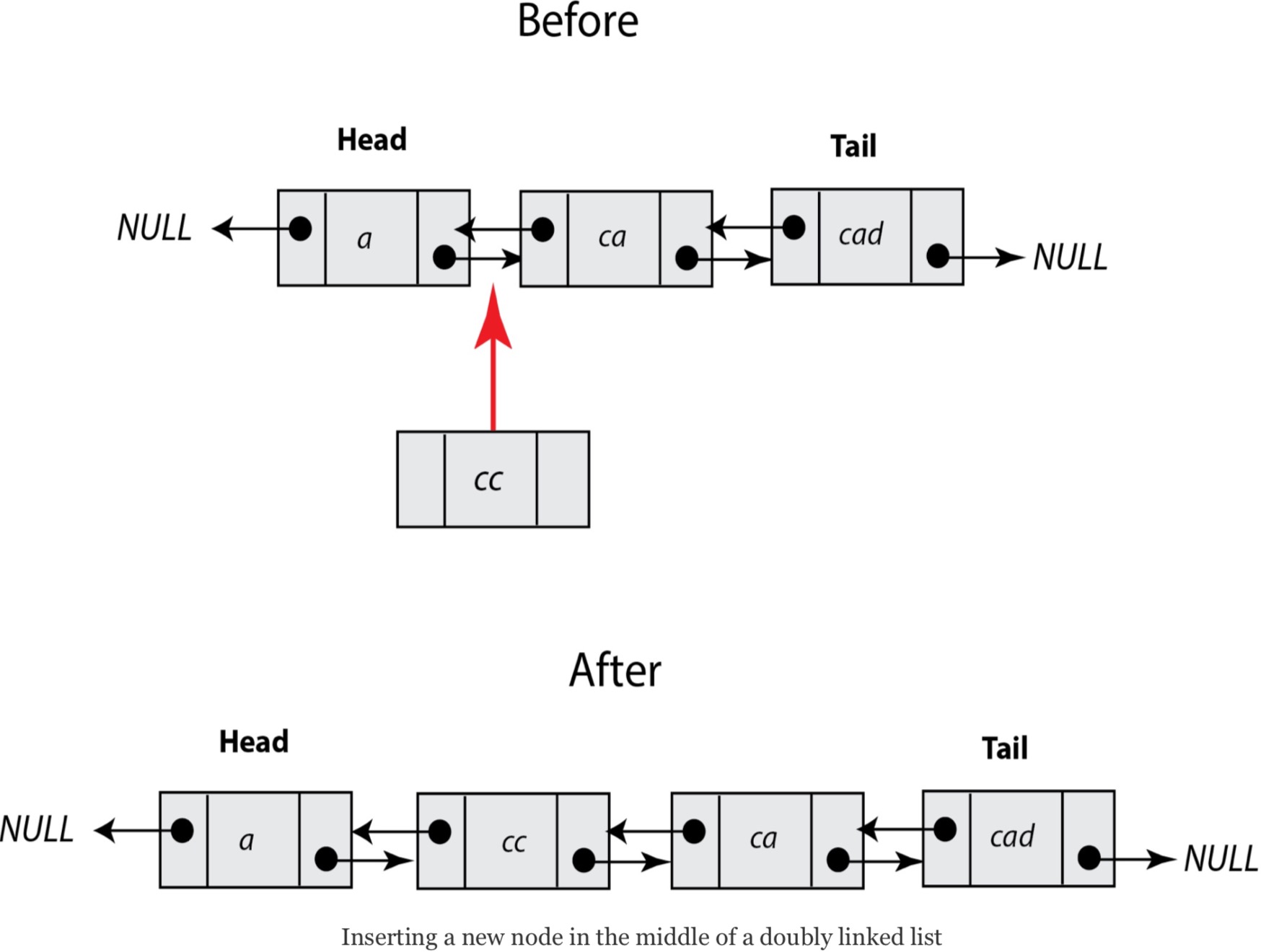
所以，单向链表和双向链表的主要区别实际上只是双向链表的操作更冗杂。这是你为了能够从两个方向都能访问双向链表所必须付出的代价。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
package main

import (
	"fmt"
)

type Node struct {
	Value    int
	Previous *Node
	Next     *Node
}

func addNode(t *Node, v int) int {
	if root == nil {
		t = &Node{v, nil, nil}
		root = t
		return 0
	}

	if v == t.Value {
		fmt.Println("Node already exists:", v)
		return -1
	}

	if t.Next == nil {
		temp := t
		t.Next = &Node{v, temp, nil}
		return -2
	}

	return addNode(t.Next, v)
}

func traverse(t *Node) {
	if t == nil {
		fmt.Println("-> Empty list!")
		return
	}

	for t != nil {
		fmt.Printf("%d -> ", t.Value)
		t = t.Next
	}
	fmt.Println()
}

func reverse(t *Node) {
	if t == nil {
		fmt.Println("-> Empty list!")
		return
	}

	temp := t
	for t != nil {
		temp = t
		t = t.Next
	}

	for temp.Previous != nil {
		fmt.Printf("%d -> ", temp.Value)
		temp = temp.Previous
	}
	fmt.Printf("%d -> ", temp.Value)
	fmt.Println()
}

func size(t *Node) int {
	if t == nil {
		fmt.Println("-> Empty list!")
		return 0
	}

	n := 0
	for t != nil {
		n++
		t = t.Next
	}
	return n
}

func lookupNode(t *Node, v int) bool {
	if root == nil {
		return false
	}

	if v == t.Value {
		return true
	}

	if t.Next == nil {
		return false
	}

	return lookupNode(t.Next, v)
}

var root = new(Node)

func main() {
	fmt.Println(root)
	root = nil
	traverse(root)
	addNode(root, 1)
	addNode(root, 1)
	traverse(root)
	addNode(root, 10)
	addNode(root, 5)
	addNode(root, 0)
	addNode(root, 0)
	traverse(root)
	addNode(root, 100)
	fmt.Println("Size:", size(root))
	traverse(root)
	reverse(root)
}

双向链表的功能比单向链表更加丰富，你可以从任意方向遍历双向链表，也可更容易地在双向链表中增删元素。此外，即使弄丢了指向双向链表头节点的指针，你也可以重新找回它。然而，这种多功能性的代价就是每个节点需要维护两个指针。开发者需要考虑这种额外的复杂性是否值得。

总之，你的音乐播放器中的歌单用的可能就是双向链表，所以你才能切换到上一首歌和下一首歌！

队列

队列是一种特殊的链表，它总是在链表头添加新的元素，在链表尾删除元素。我们不必用插图来描述队列。想象一下银行中的情形，你必须等到比你先来的人完成交易之后才能和出纳员交谈。这就是个队列！

队列最大的优点就是简单！你只需要两个函数就能访问一个队列，这意味着你需要担心的事情更少，并且你只用完成这两个函数就能实现一个队列！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
package main

import (
	"fmt"
)

type Node struct {
	Value int
	Next  *Node
}

var size = 0
var queue = new(Node)

func Push(t *Node, v int) bool {
	if queue == nil {
		queue = &Node{v, nil}
		size++
		return true
	}

	t = &Node{v, nil}
	t.Next = queue
	queue = t
	size++

	return true
}

func Pop(t *Node) (int, bool) {
	if size == 0 {
		return 0, false
	}

	if size == 1 {
		queue = nil
		size--
		return t.Value, true
	}

	temp := t
	for (t.Next) != nil {
		temp = t
		t = t.Next
	}

	v := (temp.Next).Value
	temp.Next = nil

	size--
	return v, true
}

func traverse(t *Node) {
	if size == 0 {
		fmt.Println("Empty Queue!")
		return
	}

	for t != nil {
		fmt.Printf("%d -> ", t.Value)
		t = t.Next
	}
	fmt.Println()
}

func main() {
	queue = nil
	Push(queue, 10)
	fmt.Println("Size:", size)
	traverse(queue)

	v, b := Pop(queue)
	if b {
		fmt.Println("Pop:", v)
	}
	fmt.Println("Size:", size)

	for i := 0; i < 5; i++ {
		Push(queue, i)
	}
	traverse(queue)
	fmt.Println("Size:", size)

	v, b = Pop(queue)
	if b {
		fmt.Println("Pop:", v)
	}
	fmt.Println("Size:", size)

	v, b = Pop(queue)
	if b {
		fmt.Println("Pop:", v)
	}
	fmt.Println("Size:", size)
	traverse(queue)
}

栈

栈是一种看起来像一堆盘子的数据结构。你在需要一个新盘子时会先使用最后一个被放在这堆盘子顶端的那个盘子。

栈最大的优点就是简单，因为你只需要实现两个函数就能使用栈，之后你可以向栈中添加新节点或者删除栈中的节点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
package main

import (
	"fmt"
)

type Node struct {
	Value int
	Next  *Node
}

var size = 0
var stack = new(Node)

func Push(v int) bool {
	if stack == nil {
		stack = &Node{v, nil}
		size = 1
		return true
	}

	temp := &Node{v, nil}
	temp.Next = stack
	stack = temp
	size++
	return true
}

func Pop(t *Node) (int, bool) {
	if size == 0 {
		return 0, false
	}

	if size == 1 {
		size = 0
		stack = nil
		return t.Value, true
	}

	stack = stack.Next
	size--
	return t.Value, true
}

func traverse(t *Node) {
	if size == 0 {
		fmt.Println("Empty Stack!")
		return
	}

	for t != nil {
		fmt.Printf("%d -> ", t.Value)
		t = t.Next
	}
	fmt.Println()
}

func main() {

	stack = nil
	v, b := Pop(stack)
	if b {
		fmt.Print(v, " ")
	} else {
		fmt.Println("Pop() failed!")
	}

	Push(100)
	traverse(stack)
	Push(200)
	traverse(stack)

	for i := 0; i < 10; i++ {
		Push(i)
	}

	for i := 0; i < 15; i++ {
		v, b := Pop(stack)
		if b {
			fmt.Print(v, " ")
		} else {
			break
		}
	}
	fmt.Println()
	traverse(stack)
}

container包

container 包支持三种数据结构：heap、list 和 ring。container/heap、container/list 和 container/ring 分别实现了这些数据结构。

有的人可能对环不太熟悉，环就是一个循环链表，也就是说环上的最后一个元素中的指针指向环上的第一个元素。从根本上来说，这意味着环上的每个节点都是平等的，并且没有开头和结尾。因此，从环上任一元素开始都能遍历整个环。

后面的三个小节将分别详细介绍 container 包中的每一个包。有个合理的建议：你应该先判断 Go 语言标准库 container 的功能是否满足你的需求，如果满足再加以使用，否则你应该使用自己实现的数据结构。

使用 container/heap

container/heap 实现的堆是一个树结构，树上的每个节点都是其所在子树上最小的元素。注意，我这里说的是最小的元素而不是最小的值是为了突出堆不止支持数值。

不过你可能已经猜到了，为了使用 Go 语言实现堆积树，你需要自己开发一种用来比较两个元素大小的方法。这种情况下，使用 Go 语言中的接口来定义比较合适。

这意味着 container/heap 包比 container 包中的其他两个包更加先进，而且你需要先完成一些定义之后才能使用 container/heap 包的功能。更准确地说，container/heap 包要求你实现 container/heap.Interface，其定义如下：

1
2
3
4
5
type Interface struct {
    sort.Interface
    Push(x interface{}) // 将 x 添加为第 Len() 个元素
    Pop() interface{}   // 删除并返回第 Len() - 1 个元素。
}

sort.Interface、Push() 函数和 Pop() 函数。sort.Interface 中需要实现的函数包括 Len()、Less() 和 Swap()。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package main

import (
	"container/heap"
	"fmt"
)

type heapFloat32 []float32

func (n *heapFloat32) Pop() interface{} {
	old := *n
	x := old[len(old)-1]
	new := old[0 : len(old)-1]
	*n = new
	return x
}

func (n *heapFloat32) Push(x interface{}) {
	*n = append(*n, x.(float32))
}

func (n heapFloat32) Len() int {
	return len(n)
}

func (n heapFloat32) Less(a, b int) bool {
	return n[a] < n[b]
}

func (n heapFloat32) Swap(a, b int) {
	n[a], n[b] = n[b], n[a]
}

func main() {
	myHeap := &heapFloat32{1.2, 2.1, 3.1, -100.1}
	heap.Init(myHeap)
	size := len(*myHeap)
	fmt.Printf("Heap size: %d\n", size)
	fmt.Printf("%v\n", myHeap)
	myHeap.Push(float32(-100.2))
	myHeap.Push(float32(0.2))
	fmt.Printf("Heap size: %d\n", len(*myHeap))
	fmt.Printf("%v\n", myHeap)
	heap.Init(myHeap)
	fmt.Printf("%v\n", myHeap)
}

堆是一个树状结构，而不是像数组或切片这样的线性结构

使用 container/list

container/list 包实现了链表

你可以用 list.PushBack() 函数在链表尾部插入对象，也可以使用 list.PushFront() 函数在链表的头部插入对象。这两个函数的返回值都是链表中新插入的对象。如果你想在指定的元素后面插入新的元素，那么可以使用 list.InsertAfter() 函数。类似的，你应该使用 list.InsertBefore() 在指定元素的前面插入新元素，如果指定的元素不存在链表就不会改变。list.PushBackList() 将一个链表的副本插入到另一个链表的后面。list.PushFrontList() 函数将一个链表的副本插入到另一个链表的前面。list.Remove() 函数从链表中删除一个指定的元素。

注意，使用 values.Init() 将会清空一个现有的链表或者初始化一个新的链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
package main

import (
	"container/list"
	"fmt"
	"strconv"
)

func printList(l *list.List) {
	for t := l.Back(); t != nil; t = t.Prev() {
		fmt.Print(t.Value, " ")
	}
	fmt.Println()

	for t := l.Front(); t != nil; t = t.Next() {
		fmt.Print(t.Value, " ")
	}

	fmt.Println()
}

func main() {

	values := list.New()

	e1 := values.PushBack("One")
	e2 := values.PushBack("Two")
	values.PushFront("Three")
	values.InsertBefore("Four", e1)
	values.InsertAfter("Five", e2)
	values.Remove(e2)
	values.Remove(e2)
	values.InsertAfter("FiveFive", e2)
	values.PushBackList(values)

	printList(values)

	values.Init()
	fmt.Printf("After Init(): %v\n", values)

	for i := 0; i < 20; i++ {
		values.PushFront(strconv.Itoa(i))
	}

	printList(values)
}

使用 container/ring

创建新的环需要使用 ring.New() 函数，它需要接受一个提供环的大小的参数

ring.Do() 函数可以对环上的每个元素依次调用一个函数。然而 ring.Do() 没有定义对环进行修改的行为。

使用环会遇到的唯一的问题就是你可以无限调用 ring.Next()，所以你需要找到停下来的办法。这种情况下就需要用到 ring.Len() 函数。就个人而言，我比较倾向于使用 ring.Do() 函数来迭代环上的所有元素，因为这样代码更简洁，但用 for 循环其实也不错！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
package main

import (
	"container/ring"
	"fmt"
)

var size int = 10

func main() {
	myRing := ring.New(size + 1)
	fmt.Println("Empty ring:", *myRing)

	for i := 0; i < myRing.Len()-1; i++ {
		myRing.Value = i
		myRing = myRing.Next()
	}

	myRing.Value = 2
	sum := 0
	myRing.Do(func(x interface{}) {
		t := x.(int)
		sum = sum + t
	})
	fmt.Println("Sum:", sum)
	for i := 0; i < myRing.Len()+2; i++ {
		myRing = myRing.Next()
		fmt.Print(myRing.Value, " ")
	}
	fmt.Println()
}

生成随机数

随机数的生成是计算机科学的一个研究领域，同时也是一种艺术。这是因为计算机是纯粹的逻辑机器，所以使用计算机生成随机数异常困难！

你可以用 math/rand 包来生成随机数。开始生成随机数之前首先需要一个种子，种子用于整个过程的初始化，它相当重要。因为如果你每次都用同样的种子初始化，那么就总是会得到相同的随机数序列。这意味着每个人都可以重新生成同一个序列，那这个序列就根本不能再算是随机的了！

我们将用来生成随机数的程序名为 randomNumbers.go，下面分成四个部分进行介绍。这个程序需要几个参数，分别是生成随机数的下限、生成随机数的上限、生成随机数的数量。如果你还用了第四个命令参数，那么程序会将它作为随机数生成器的种子。在测试的时候，你就可以再次使用这个参数生成相同的数列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
package main

import (
	"fmt"
	"math/rand"
	"os"
	"strconv"
	"time"
)

func random(min, max int) int {
	return rand.Intn(max-min) + min
}

func main() {
	MIN := 0
	MAX := 100
	TOTAL := 100
	SEED := time.Now().Unix()

	arguments := os.Args
	switch len(arguments) {
	case 2:
		fmt.Println("Usage: ./randomNumbers MIN MAX TOTAL SEED")
		MIN, _ = strconv.Atoi(arguments[1])
		MAX = MIN + 100
	case 3:
		fmt.Println("Usage: ./randomNumbers MIN MAX TOTAL SEED")
		MIN, _ = strconv.Atoi(arguments[1])
		MAX, _ = strconv.Atoi(arguments[2])
	case 4:
		fmt.Println("Usage: ./randomNumbers MIN MAX TOTAL SEED")
		MIN, _ = strconv.Atoi(arguments[1])
		MAX, _ = strconv.Atoi(arguments[2])
		TOTAL, _ = strconv.Atoi(arguments[3])
	case 5:
		MIN, _ = strconv.Atoi(arguments[1])
		MAX, _ = strconv.Atoi(arguments[2])
		TOTAL, _ = strconv.Atoi(arguments[3])
		SEED, _ = strconv.ParseInt(arguments[4], 10, 64)
	default:
		fmt.Println("Using default values!")
	}
	rand.Seed(SEED)
	for i := 0; i < TOTAL; i++ {
		myrand := random(MIN, MAX)
		fmt.Print(myrand)
		fmt.Print(" ")
	}
	fmt.Println()
}

如果需要用 Go 生成更安全的随机数的话，你可以使用 crypto/rand 包。这个包中实现了满足密码学安全的伪随机数生成器。你可以在 https://golang.org/pkg/crypto/rand/ 文档页面了解更多关于 crypto/rand 包的信息。